Two dimensional shapes can be drawn on a flat surface. It is a shape that has two measurements: length and width. Common 2d shapes include a rectangle, pentagon, circle and triangle. They are introduced in primary school and expanded upon in your GCSE exams. You are expected to know their properties - such as angles and sides - and be able to calculate perimeter and area.
This article will begin by explaining shapes in two dimensions and how you can calculate their perimeter and area. We will explore key properties of these shapes, including symmetry. Practice examples will be tackled step-by-step and quiz questions are included to test your knowledge. This guide is suitable for students revising for their GCSE exams, including AQA and OCR.
If you want help, TeachTutti has GCSE Maths tutors who can support your learning about 2d shapes. Lessons can be online or in-person.
What are Two Dimensional shapes?
2d shapes are flat and only measure length and width. They are drawn completely flat on a single plane, like a piece of paper. 2d and 3d shapes differ in that they don't have any depth. 2d shape names include:
- Triangles (3 sides).
- Quadrilaterals (4 sides), such as squares and rectangles.
- Pentagons, hexagons and octagons.
There are fundamental properties of 2d shapes. Understanding these properties helps us calculate area, perimeter, symmetry and questions involving compound shapes:
- Regular 2d shape - A shape that has equal sides and angles.
- Irregular 2d shape - The sides and angles are not the same.
- Polygon - Closed figures made from straight lines e.g. a square is a polygon and a circle is not.

1
What shape is not a polygon?
Polygons: Regular and irregular
A polygon is a 2d shape made from straight lines. It is called a closed shape because all the lines connect with no gaps. These shapes include triangles, rectangles, pentagons and hexagons.
There are two types of polygons:
- Regular polygon - All sides are equal in length and all the angles measure the same. For example, a square is a regular polygon because all four sides are equal in length and all four angles are 90 degrees.
- Irregular polygon - The straight sides and angles are not all the same. A rectangle is a 2d shape that is irregular. Another example is a scalene triangle, which has three sides of different lengths.

2
Which shape is a regular polygon?
Area and Perimeter
Perimeter
The perimeter is the total distance around the outside edges of a shape. To find this value, you need to add all the lengths together. Remember to use a standard unit in your calculation, depending on the size of the shape, e.g. millimetres (mm), centimetres (cm), or metres (m).
For example:
- A square has a length of 5cm for each side. The perimeter is 20 cm (5 + 5 + 5 + 5).
- A rectangle has a length of 8cm and a width of 3cm. The perimeter is 22cm (2 × (8 + 3)).
- If you are using a compound shape (made from more than one shape), label each side and add up the edge lengths.
- For compound shapes (made from more than one basic shape), the process is the same: label each side and add up all the edge lengths. Watch out for missing sides that you may need to calculate first.
Perimeter is often used when solving practical issues, such as fencing a garden or the trim needed for a picture frame.
3
What is the perimeter of a rectangle with a length of 12cm and a width of 7cm?
Area of 2d shapes, including triangles and rectangles
The area of 2-d shapes is how much space they cover. This distinguishes it from the perimeter, which measures the distance around the edge. It is measured in square units, depending on the size of the shape. For example, square centimetres (cm²), square metres (m²), or square millimetres (mm²). There are area formulas you will need to know for different 2D shapes. We have listed the most common below:
Squares and rectangles
- Area of a square = side × side.
- Area of a rectangle = length × width.
- For example, a rectangle has an 8cm length and 3cm width. The area is 24cm² (8 × 3).

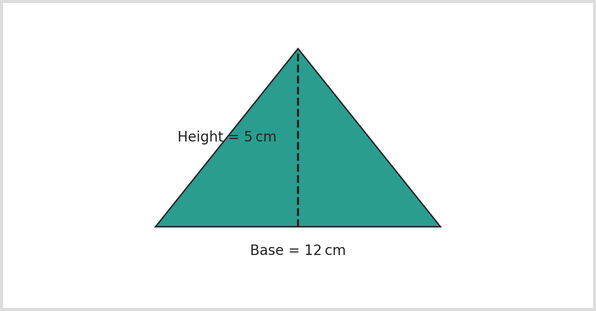
Triangles
- Triangles take up half the area of a rectangle with the same base and height.
- Area of a triangle = 1/2 × base × height.
- They take up half the area of a rectangle that has the same base and height. Make sure to use the vertical height with the formula above, not the slanted side.
- For example, a triangle has a 10cm base and a 4cm height of 4cm. The area is 20cm² (1/2 × 10 × 4).
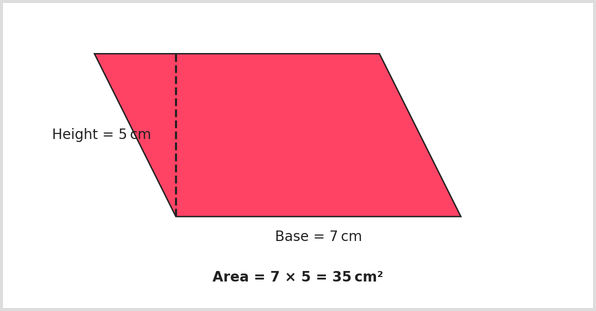
Parallelograms
- Area of a parallelogram = base × perpendicular height.
- A parallelogram is a slanted rectangle. For this reason, the formula is the same as that of a rectangle. The perpendicular height matters, not the slanted side.
- For example, a parallelogram has a 7cm base and a 5cm height. The area is 35cm² (7 X 5).
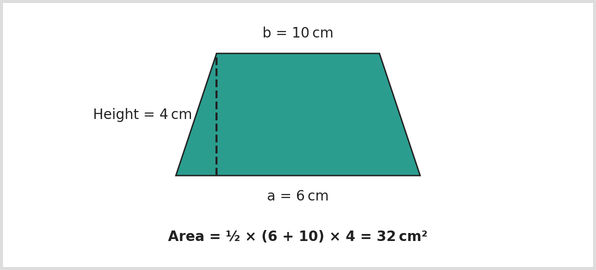
Trapeziums
- Area of a trapezium = 1/2 × (a + b) × height.
- A trapezium has two parallel sides (named a and b), with a height between them.
- For example, let's say a trapezium has parallel sides of 6cm and 10cm and a height of 4cm. The area is 32cm² (1/2 × (6 + 10) × 4 = 1/2 × 16 × 4).
Compound shapes
Compound shapes are made up of two or more simple shapes joined together. Take the following steps to find the area:
- Split the shape into its shapes, such as rectangles or triangles.
- Work out the area of each one.
- Add them together to get the total area.
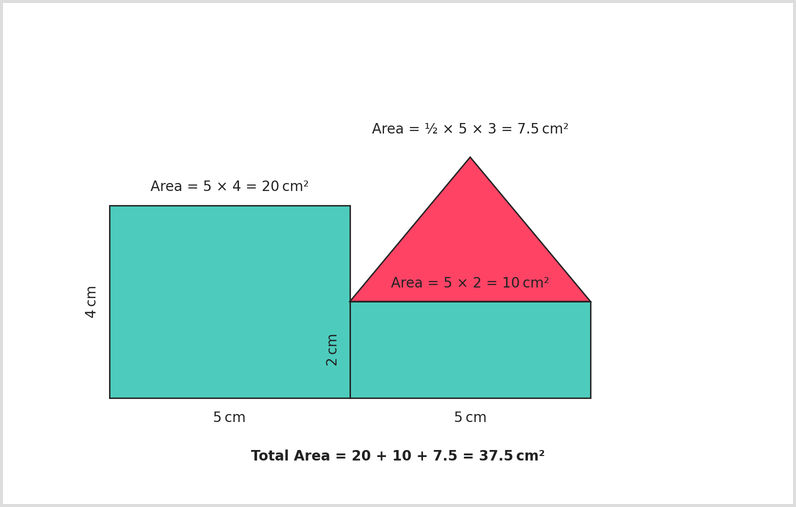
You may need to subtract an area, such as if part of the shape is missing or cut out.
4
A trapezium has parallel sides of 4cm and 6cm, with a height of 5cm. What is its area?
Properties of 2d shapes - Symmetry and angles
Symmetry
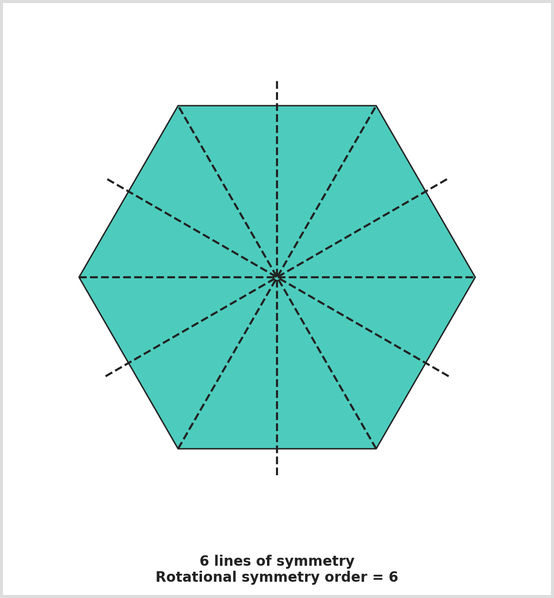
There are two main types of symmetry:
- Line symmetry - This is also known as reflectional symmetry. This is when a shape can be folded along a line and both sides match exactly.
- Rotational symmetry - This is a shape that can be rotated around its centre and look the same before it has rotated 360 degrees.
For example, the following 2d shapes have symmetry:
- A square has 4 lines of symmetry and rotational symmetry of order 4.
- An equilateral triangle has 3 lines of symmetry and rotational symmetry of order 3.
- A scalene triangle has no symmetry at all.
Angles in polygons
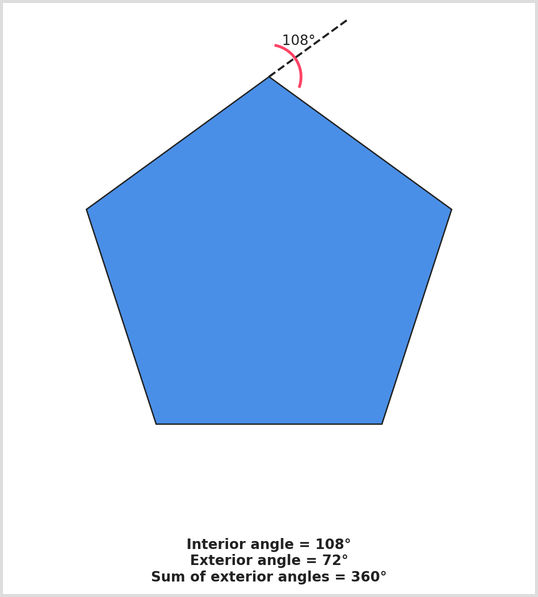
You need to be able to calculate interior and exterior angles in polygons. Interior angles are the angles inside a polygon. Exterior angles are created between one side of the shape and the extension of the next side.
This is the formula to calculate the total of the interior angles in any polygon: Sum of interior angles = (n - 2) × 180° (n is the number of sides).
This is the formula to find one interior angle of a regular polygon (all angles are the same): Interior angle = [(n - 2) × 180°] / n
Remember that the sum of all exterior angles in a polygon must always equal 360 degrees.
For example, a regular pentagon has 5 sides. The sum of interior angles is 540 degrees (5 - 2) x 180. Each interior angle equals 108 degrees (540 / 5).
5
How many lines of symmetry does a regular hexagon have?
Solved examples of 2d shapes
It's helpful to see how questions on types of 2d shapes are solved in stages. We have provided worked examples involving two-dimensional shapes that often appear in GCSE Maths exams.
Example 1: Area of a trapezium
Find the area of the trapezium below.
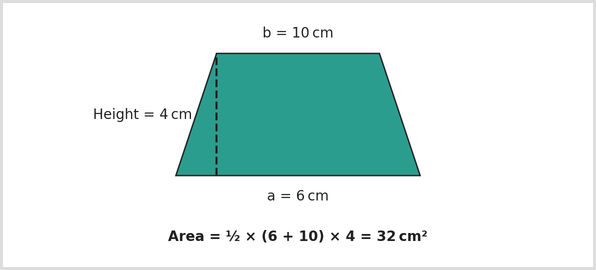
- Use the formula | Area of a trapezium = 1/2 × (a + b) × height
- Substitute values | a = 6cm, b = 10cm, height = 4cm. Area = 1/2 × (6 + 10) × 4
- Calculate | 1/2 × 16 × 4 = 8 × 4 = 32cm²
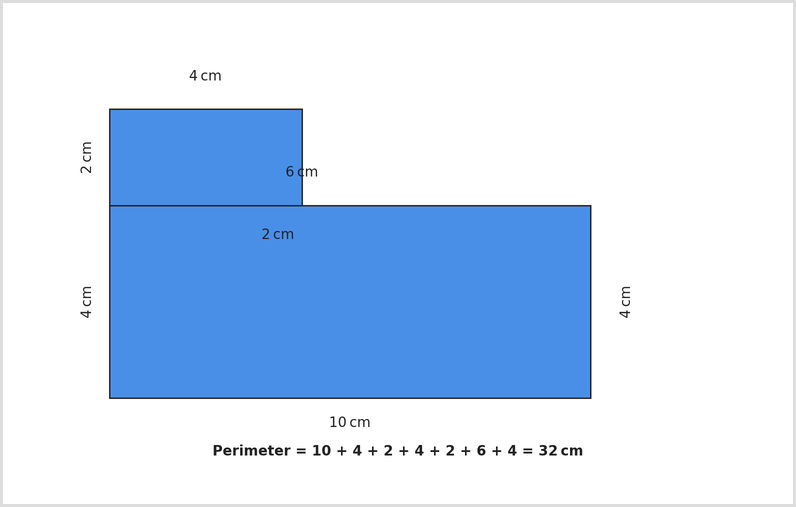
Example 2: Perimeter of a compound shape
Work out the perimeter of the compound shape made from two rectangles.
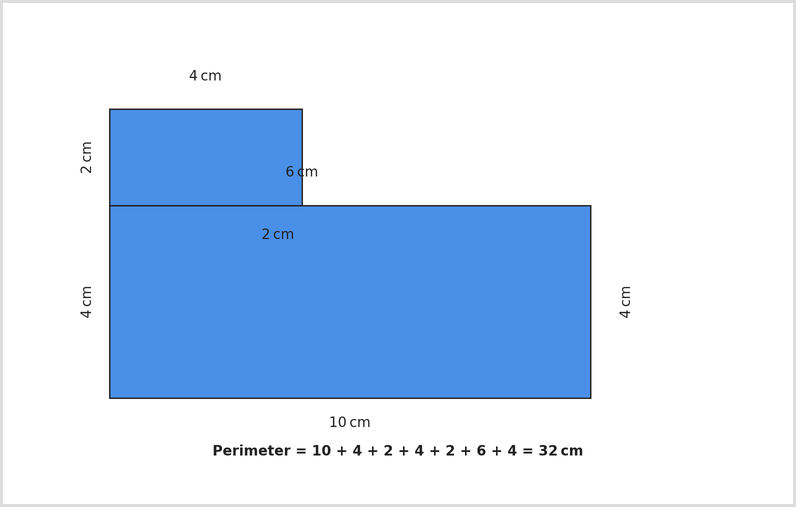
- Find and label all side lengths | Check if any sides are missing. Use known values to work them out.
- Add up all outer edges | Perimeter = 10 + 4 + 2 + 4 + 2 + 6 + 4 = 32cm
Example 3: Angles in a Regular Polygon
A regular octagon has 8 sides. Find the size of one interior angle.
![Worked Example: Interior Angle of a Regular Octagon A regular octagon with one interior angle highlighted in green and labelled as 135°. Below the shape, the calculation is shown using the formula: Interior angle = [(8 ? 2) × 180] ÷ 8 = 135°.](https://ik.imagekit.io/mpa1ue4fhzq8/Blog/output__4__Wfb8T9816.png/tr:b-3_DDDDDD,w-0.5)
- Use the angle formula | Interior angle = [(n - 2) × 180°] / n = [(8 - 2) × 180] / 8 = (6 × 180) / 8 = 1080 / 8 = 135°
Practice Questions - 2d geometric shapes
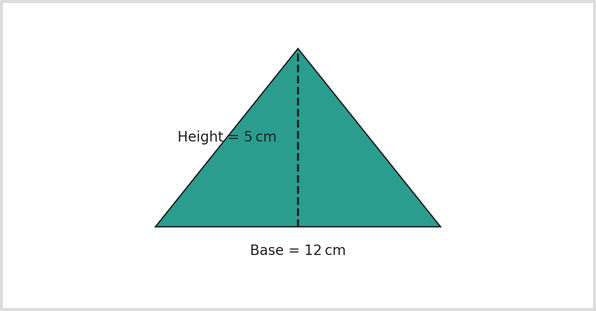
6
A triangle has a base of 12cm and a vertical height of 5cm. What is the area of the triangle?
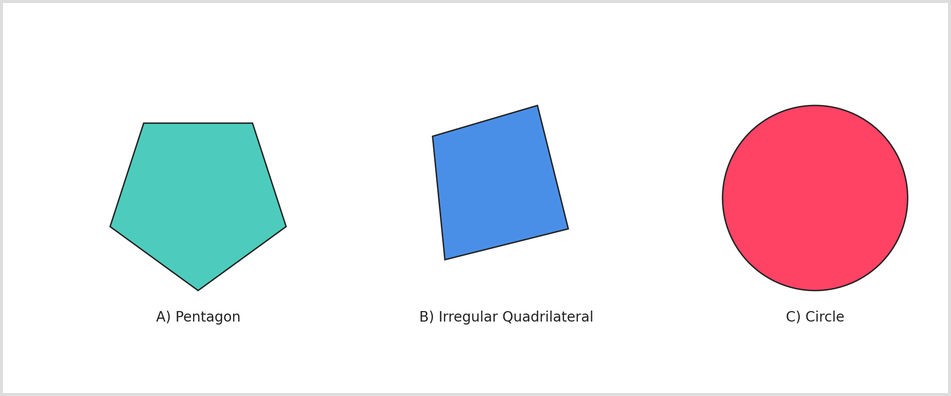
7
Which shape is a regular polygon?
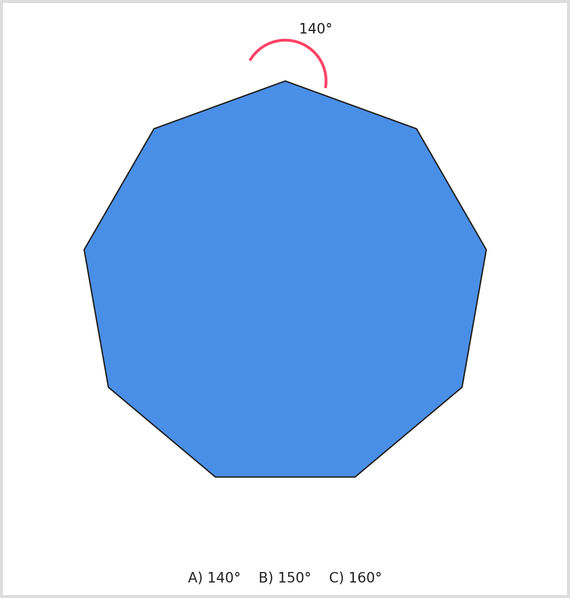
8
A regular nonagon has 9 equal sides. What is the size of one interior angle?
9
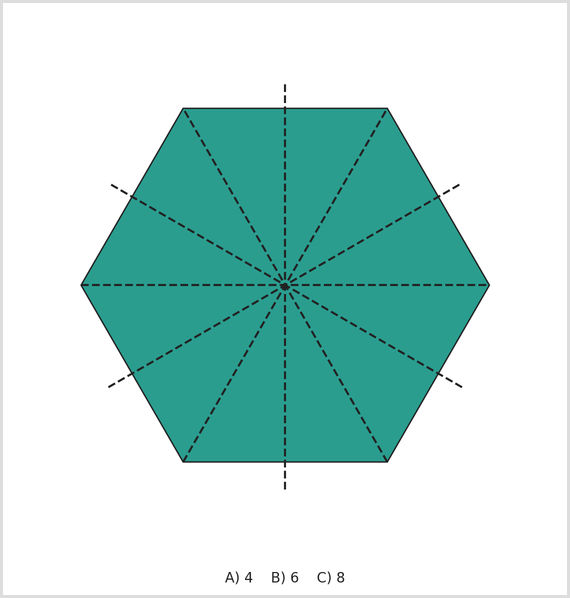
How many lines of symmetry does this shape have?
Common mistakes
There are a few pitfalls to watch out for when tackling GCSE questions on 2d shapes. We have covered the most common mistakes to look out for so you can save marks and feel more confident approaching these questions.
Mixing up perimeter and area - Perimeter is the distance around the edge of a shape. Area is the amount of space inside the shape. The perimeter is normally measured in centimetres or metres, while area is squared, such as square centimetres (cm²) or square metres (m²).
For example, let's say a square has 6 cm sides. The perimeter is 24 cm (6 × 4) and the area is 36cm² (6 x 6).
Using the wrong height - Make sure you use the perpendicular height, which is at 90 degrees to the base. Don't use slanted or diagonal lengths unless the exam questions direct you to. This issue is most common with triangles, trapeziums and parallelograms.
Forgetting to include units - Ensure you use the correct unit in your answer. For example, if the answer to the area is "36", this is incorrect as you need to give the measurement, such as "36cm²". Otherwise, you risk losing marks.
Assuming quadrilaterals are rectangles - Not all quadrilaterals are rectangles, e.g. parallelograms, trapeziums, rhombuses and kites. Each shape has different properties and different formulas. Make sure you know the shape you're working with. Never assume and always double-check.
Final thoughts on 2d shapes
This article has explained the different types of 2d shapes and their properties, such as symmetry. For example, we now know that 2d shapes are distinguishable from 3d shapes because they are flat and can only be measured by width and length. We have covered common GCSE questions related to this topic, such as calculating the area of a compound shape, identifying symmetry, or applying angle rules in polygons.
For extra practice with flashcards and memory tools, you can check out Quizlet’s GCSE Maths resources on geometry shapes. You may also want to challenge yourself with past exam questions on 2d shapes by MathsGenie.
If you’d like more support, TeachTutti have GCSE Maths tutors who can guide your revision. Every tutor has an enhanced DBS check and lessons are tailored to your learning. Tuition can be online or in-person.

