Straight line graphs show a linear equation that depicts a relationship between quantities. This is a topic in GCSE Maths that uses algebra and geometry. These illustrations are often used to show how this relationship changes over time e.g. predicting the cost of a phone bill based on the number of text messages sent. It involves calculating gradients, the equation y=mx+c and plotting points on a coordinate grid.
This guide looks at the basics, including how to draw a straight-line graph and the equation of a straight line graph. It is aimed at students preparing for their examinations and is suitable for AQA and Edexcel. If you need further support with your GCSE Maths revision, TeachTutti has experienced GCSE Maths tutors who can help you learn and revise this topic.
Learn the basics of Straight Line Graphs
Algebra and geometry are combined for this topic. The graphs show linear equations, which describe a constant rate of change between two variables. The straight line equation is y = mx + c:
- m - This is the gradient, which measures the slope of the line. A higher gradient makes the line steeper. If the gradient is zero, the line is horizontal.
- c - This is the y-intercept. It is when the line crosses the y-axis.
Types of Straight Line Graphs
- Positive gradient: The line slopes upwards as you move from left to right. For example, the equation y = 2x + 1 has a positive gradient of 2.
- Negative gradient: The line slopes downwards as you move from left to right, such as y = -3x + 4.
- Zero gradient: This is a flat, horizontal line where y = c. For example, y = 5.
- Undefined gradient: A vertical line that doesn't follow the equation y = mx + c. For example, x = 3.
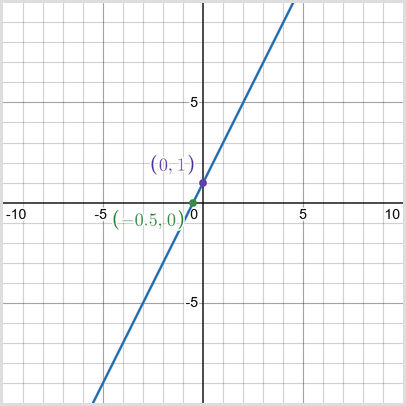
Example 1
The straight line graph below uses the equation y = 2x+1:
- The y-intercept is (0,1), where the line crosses the y-axis.
- The x-intercept is (-0.5,0), where the line crosses the x-axis.
- The equation y=2x+1 means the gradient (m) is 2 and the y-intercept (c) is 1.
This graph shows the mix of algebra and graphical representation. We can see the gradient (m=2) because the line rises 2 units for every 1 unit it moves to the right.
These graphs are used in a variety of real-world situations:
- Business - They are used to predict the profits of a company based on sales.
- Science - They show the relationship between two quantities in an experiment e.g. temperature and time.
- Transport - Speed can be calculated using distance-time graphs.
1
What is the gradient and y-intercept of the line shown by y = -4x + 3?
Plot a Straight Line Graph
Plotting a straight line graph means putting points on the line at exact positions. Here is a step-by-step approach to this process:
Step 1: Equation
Make sure the equation is in the form y = mx + c. Breaking this down, m is the gradient and c is the y-intercept. For example, y = 2x + 1 means:
- The gradient is 2. The line rises 2 units for every unit it moves to the right.
- The y-intercept is 1. This means the line crosses the y-axis at (0,1).
Step 2: Table of values
Choose a range of x-values. Substitute them into the equation and calculate the related y-values. For example, in the equation y = 2x + 1, could use the the x values -2, -1, 0, 1, 2:
| x | y=2x+1 | (x,y) |
| -2 | 2(-2) + 1 = -3 | (-2,-3) |
| -1 | 2(-1) + 1 = -1 | (-1,-1) |
| 0 | 2(0) + 1 = 1 | (0,1) |
| 1 | 2(1) + 1 = 3 | (1,3) |
| 2 | 2(2) + 1 = 5 | (2,5) |
Step 3: Plot the points
Plot the points on a coordinate grid using the table of values. These are (-2,-3), (-1,-1), (0,1), (1,3) and (2,5). Make sure the axes are labelled and scaled.
Step 4: Draw the line
Use a ruler to connect the points with a straight line. Extend the line to each end of the graph and use arrows to show it continues indefinitely. Label the line with its equation y = 2x + 1.

2
What is the y-coordinate when x = 2 on the line y = 3x - 2?
Understand the gradient
The gradient is also called the slope. It tells us how steep the line will be and whether it will slope upwards, downwards, or be horizontal.
What is the gradient?
The gradient of a line is shown by m in the equation y = mx + c. It measures how much the y-value (vertical change) changes for each unit of change in the x-value (horizontal change). The formula is m = change in y / change in x = change in y / change in x.
As an example, let's say the line passed through the points (0,1)and (2,5). This can be expressed as m = 5 -1 / 2 - 0 = 4 / 2 = 2. This means that for every unit the line moves to the right, it will also rise by 2 units.
Types of gradients
- Positive gradient - The line slopes upward from left to right e.g. y = 2x + 1 has a positive gradient of 2.
- Negative gradient - The line slopes downward from left to right e.g. y = -3x + 4 has a negative gradient of -3.
- Zero gradient - This means the line is horizontal. For example, y = 5 is a zero gradient because the gradient m = 0.
- Undefined gradient - The line is vertical e.g. x = -2. Vertical lines don't have a gradient because the change in x is 0. This means the formula change in y / change in x is undefined.
Here are a few places we see gradients in daily life:
- Roads - A steep road has a high gradient, making it difficult to drive up and requiring for acceleration.
- Finance - A positive gradient on a profit graph means the company has increasing earnings. Meanwhile, a negative gradient indicates losses.
- Science - Gradients on graphs can show rates of change e.g. speed on a distance-time graph.
Example 2
Try to find the gradient of a line that passes through the points (-1,2) and (3,10).
- Use the formula m = change in y / change in x.
- Find out the differences between these points. The difference in y is 10 - 2 = 8. The different in x is 3 -(-1) = 3 + 1 = 4.
- Divide the x and y values to find the answer: m = 8 / 4 = 2. This means the gradient is 2.
3
The gradient of a line is -3. Which two points can the line pass through?
The Y-intercept
The y-intercept is where the line crosses the y-axis - it's a starting point for drawing the line. This is the value of y when x = 0.
In the equation y = mx + c, the constant c is the y-intercept. For example, this value is 2 in y = 3x + 2. It is -5 in the equation y = -4x - 5.
The y-intercept is always written as a coordinate, (0,c). For example, if c = 2, the y-intercept is written as (0,2). If c = -5, the y-intercept is (0,-5).
Find the Y-intercept
There are two ways to find out the value of the y-intercept:
- Use the equation - You just need to find c in the equation form y = mx + c. For example, the y-intercept is 3 in y = 5x + 3.
- Use the graph - Find where the line crosses the y-axis (where x=0) and note the y-coordinate. For example, the y-intercept is -1 on the graph of y=2x-1. This is because the line crosses the y-axis at (0,-1).
Applications of the Y-intercept
The y-intercept can be used in a variety of practical scenarios:
- Business: In cost equations like y = mx + c. Here c represents fixed costs, like rent.
- Physics: In motion graphs, the y-intercept could show the starting position of an object.
- Finance: The y-intercept shows the starting amount when graphing savings or investments.
Example 3
Try to find the y-intercept of the line that passes through the points (-2,-4) and (2,4):
- Find the gradient m: m = change in y / change in x = 4-(-4) / 2-(-2) = 8 / 4 = 2
- Use the equation y = mx + c. Substitute m = 2 and one point, like (2,4): 4 = 2(2) + c
- All you need to do now is simplify the equation: 4 = 4 + c -> c = 0
This means the y-intercept is c = 0 or (0,0).
4
What is the y-intercept of the line y = -5x + 7?
Parallel and perpendicular lines
Straight line graphs also show how lines interact with each other. Two of these interactions are parallel and perpendicular lines, both defined by their gradients.
Parallel lines
Parallel lines run in the same direction as each other. They never meet, regardless of their length. They have the same gradient(m) but different y-intercepts (c). For example, the lines y = 3x + 2 and y = 3x - 4 are parallel because they both have a gradient of 3. The equation for parallel lines is m1 = m2.
Perpendicular lines
Perpendicular lines intersect at a right angle (90 degrees). Their gradients are negative reciprocals of each other. Written as an equation, perpendicular lines are m1 × m2 = -1. For example, if a line has the equation y = 2x + 1 (m1 = 2), a perpendicular line could have the equation y = - 1 / 2x + 4 (m2 = - 1 / 2).
Equations of parallel and perpendicular lines
- Parallel lines - Make sure the gradient is the same as the original line. Only adjust the y-intercept. For example, try to find a line parallel to y = 4x - 3 passing through (2,5). The gradient is 4 (y = 4x + c). Next, substitute (2,5): 5 = 4(2) + c -> 5 = 8 + c -> c = -3. This means the equation is y = 4x - 3
- Perpendicular lines - Use the negative reciprocal of the gradient. For example, try to find a line perpendicular to y = 3x + 2 passing through (1,4). Firstly, the gradient is -1 / 3 (y = - 1 / 3 x + c). Next, substitute (1,4): 4 = - 1 / 3 (1) +c -> 4 = - 1 / 3 + c -> c = 4 + 1 / 3 = 13 / 3. Therefore, the equation is y = - 1 / 3 x +13 / 3
Applications of parallel and perpendicular lines
These are some of the ways parallel and perpendicular lines are used in the world around us:
- Construction: To keep walls, beams and edges properly aligned.
- Maps and navigation: Roads and railway tracks often use parallel or perpendicular patterns.
- Design: Graphic designers use these lines to create balanced, aligned layouts.
Example 4
Try to work out if the lines y = -2x + 1 and y = 12x - 3 are perpendicular.
- Find the gradients: line 1 is m1 = -2, while line 2 is m2= 1 / 2
- Check that m1 × m2 = -1. (-2) × 1 /2 = -1
Yes, the lines are perpendicular.
5
Which line is parallel to y = 5x - 4?
Common mistakes
Small mistakes can lead to incorrect results when working with these graphs. We have discussed common mistakes to be aware of, so you can instead use best practices and build confidence in the topic:
1. Misinterpret the gradient
The gradient (m) describes how steep the line will be. It is common to confuse the positive or negative direction of a gradient. A positive gradient is when the line slopes upwards e.g. y = 2x + 1. A negative gradient is when the line slopes downwards e.g. y = -3x + 4.
2. Plotting points
Be careful when plotting points from a table of values. Mistakes can happen by accidentally swapping x-coordinates and y-coordinates or by misreading scales on the graph. Make sure to double-check your plotted points and use grid lines for accuracy.
3. Extend the line
A student may sometimes draw only the segment of the line that connected the calculated points. Remember to extend the line across the graph in both directions. Add arrows at the ends to show the line continues indefinitely.
4. Horizontal and vertical lines
The horizontal (y) and vertical lines (x) are often mixed up. Remember that for horizontal lines, the y-value is constant, while the x-value is constant for vertical lines, regardless of their counterpart. Another tip is that horizontal lines have m = 0, while vertical lines have an undefined gradient.
5. Rearrange equations
An equation has to be rearranged if it doesn't use the form y = mx + c. If you don't do this or make a mistake in changing the equation, it can lead to incorrect results. Make sure to isolate y step-by-step to ensure your calculations are correct.
Example 5
Try to find the mistake in the following scenario. A student has to find the gradient of a line passing through (1,3) and (4,9). This is the student's calculation:
- m = 3 - 9 / 1 - 4 = -6 / -3 = -2
The mistake is a sign error. Both the numerator and denominator are negative. This means the gradient should return as positive: m = -6 / -3 = 2
6
What is the equation for a horizontal line passing through (0, -5)?
Final thoughts - Straight line graphs revision
We have covered the fundamentals of straight line graphs for GCSE Maths, including their use in the real world, such as in science and business:
- Equation of a line: The general form y=mx+c tells us the gradient (m) and y-intercept (c). These are the main components in a straight line graph.
- Gradient: This is how steep a line is. It is calculated as change in y / change in x. It decides if the line will slope up, down, or stay flat.
- Y-intercept: This is where the line crosses the y-axis point. It is shown by y when x = 0.
- Plotting: Putting points on a line and extending the line indefinitely across the graph.
- Parallel and perpendicular lines: It is important to be able to understand the relationship between these lines so we can analyse line interactions and solve related problems.
You can test your knowledge of this topic by using MathsGenie's Edexcel Straight Line worksheets. You can also draw a straight line graphs using Desmos, such as the illustration given at the top of this article.
If you need support learning this topic, TeachTutti has GCSE Maths Tutors who are qualified and DBS-checked. Lessons can be online or in-person.
Glossary
- Gradient - The measure of how steep a line is. It's calculated as the ratio of the vertical change (change in y) to the horizontal change (change in x).
- Y-intercept - The point when the line crosses the y-axis. It is represented by the constant c in the equation y = mx + c.
- X-intercept - The point when the line crosses the x-axis. This is found by setting y = 0 in the equation of the line.
- Linear equation - This equation makes a straight line plotted on a graph. The equation is y = mx + c.
- Coordinate - A pair of numbers that show where a point is on a graph. It's written as (x,y).
- Origin - This is the place where the x-axis and y-axis meet on a coordinate grid.
- Parallel lines - Lines never meet because they have the same gradient.
- Perpendicular lines - Lines that meet at a right angle (90 degrees). The gradients are negative reciprocals of each other.
- Delta - This symbol shows the difference in a value. Change in y means a change in y and change in x is a change in x.
- Right-angled triangle - This triangle is created when showing the gradient between two points.
- Intercept - When a line crosses the x-axis or y-axis on a graph.
- Axes - The horizontal (x) and vertical (y) lines that create a graph.
- Plotting - Putting points on a graph based on their x and y coordinates.
- Negative reciprocal - A mathematical relationship where two numbers are multiplied to -1. It defines the gradients of perpendicular lines.
- Coefficient - A number in a term of an equation. In y = mx + c, m is the coefficient of x, which decides the gradient of the line.

