A mathematical proof is a statement that is always true, no matter the numbers used. It underpins many advanced mathematical concepts and appears in various topics, such as algebraic proof - where numbers are represented with symbols - and geometric proof - which uses shape properties and theorems.
This GCSE maths revision guide will explain what proof means in maths. We will explore the types of proof used in exam questions and work through step-by-step examples to build your confidence. It is suitable for all major exam boards, including AQA and Edexcel.
If you need further support, TeachTutti has GCSE Maths tutors to help you understand this topic.
What is a Mathematical Proof?
A mathematical proof is an argument that shows a statement is always true. It is a sequence of steps that rely on mathematical rules and lead to a conclusion. A proof works in all possible cases, regardless of the numbers given. It is how we confirm a mathematical fact.
If we say that "The sum of two even numbers is always even". We can test this in numerous ways:
- 2 + 4 = 6 (even)
- 10 + 8 = 18 (even)
- 100 + 42 = 142 (even)
These examples support the statement, but they don’t prove that it will always be true. Instead, we can generalise using algebraic proof, which guarantees the statement is valid for any even numbers:
- Two even numbers can be shown as 2n and 2m. The n and m are whole numbers and the 2 shows that every even number is a multiple of 2.
- Add them together: 2n + 2m = 2(n + m)
- The sum remains a multiple of 2 because n+m is also a whole number. This means it is always even.
- For example, 2 x 3 + 2 x 8 = 2 x (3 + 8) = 22
Using proofs in maths is important because it can confirm results with certainty, whereas estimation and testing examples leave the possibility of exceptions. It also encourages logical thinking and forms the basis of advanced maths, including higher study and real-world applications like computing and engineering.
1
What is a mathematical proof?
Types of Proof
There are several types of proof in GCSE Maths. Each method uses a different approach to present its argument.
1. Direct Proof
This is the most common type of proof. The direct proof follows a logical sequence of steps to present its argument.
Example: Prove that the sum of two odd numbers is always even.
- Begin by showing two odd numbers as 2n + 1 and 2m + 1. The n and m are whole numbers
- Add them together: (2n + 1) + (2m + 1) = 2n + 2m + 2
- Factor out the 2: 2(n + m + 1)
- The result will be a multiple is 2 because n + m + 1 is a whole number. This means it is always even.
- For example, let's use the odd numbers 5 and 7. 5 = 2(2) + 1, so n=2. 7 = 2(3) + 1, so m = 3. We need to add them together and factor out the 2. 2(2) + 1 + 2(3) + 1 = 4 + 1 + 6 + 1 = 12.
2. Proof by Exhaustion
As the name implies, proof by exhaustion checks all the possible cases to confirm a statement. This method is normally used when there are a limited number of possibilities.
Example: Prove a prime number between 1 and 10 is always either 2, 3, 5, or 7.
- List all numbers from 1 to 10: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
- Find the prime numbers: 2, 3, 5, 7.
- This statement is exhaustively checked. It's true because all the other numbers are divisible by a smaller number and therefore not prime.
3. Proof by Contradiction
This method assumes the opposite of a statement is true. It shows that this leads to a contradiction, proving the original statement is true.
Example: Prove there is no largest even number.
- Assume the opposite with a counterexample: try to find the largest even number. We call this number N.
- Consider N + 2, which is also even.
- N + 2 contradicts the assumption that there is a largest even number. This is a contradiction because N was supposed to be the largest even number.
- This shows the opposite assumption, proving there isn't a largest even number.
2
Which type of proof assumes the opposite of a statement to show it leads to a contradiction?
Algebraic Proof - Examples included
Algebraic proof proves math statements using algebraic expressions and manipulation, particularly those using numbers, sequences and identities.
Key techniques
You must be confident using algebraic techniques to solve algebraic proof questions. The following techniques are required:
- Expanding brackets - This can manipulate expressions before simplifying.
- Factorising - Useful to find common multiples and prove divisibility.
- Working with consecutive numbers - Helps to prove results that use number patterns.
Example 1: Proving a number property
Prove that the sum of three consecutive integers is always a multiple of 3.
- First, show the three consecutive integers as n, n + 1 and n + 2.
- Add these integers together: n + (n + 1) + (n + 2) = 3n + 3
- Factorise the expression: 3(n + 1)
- The sum is always a multiple of 3 because n + 1 is always an integer.
For example, let's use 4, 5 and 6. First, we add them together: 4 + 5 + 6 = 15. The proof holds because 15 is a multiple of 3.
Example 2: Proving a product rule
Prove that the product of two odd numbers is always odd.
- Begin by representing two odd numbers as 2n + 1 and 2m + 1. The n and m are whole numbers.
- Multiply the odd numbers together: (2n+1)(2m+1) = 4nm + 2n + 2m + 1
- Factor out a 2 from the first three terms: 2(2nm + n + m) + 1
- The expression can be written as 2k + 1 because 2nm + n + m is always an integer. This represents an odd number.
- For example, let's use the odd numbers 7 and 9. 7 = 2(3) + 1, so n = 3. 9 = 2(4) + 1, so m = 4. We then multiply them together: 7×9=63. The proof is correct because 63 is an odd number.
Example 3: Proof with even and odd numbers
Prove that the square of an odd number is always odd.
- Represent an odd number as 2n + 1.
- Square the odd number: (2n+1)2 = 4n2 + 4n + 1
- Factor out a 2 from the first two terms: 2(2n2 + 2n) + 1
- The result follows the form 2k + 1, because 2n2 + 2n is an integer. This means it is always odd.
- For example let's use the odd number 7. 7 = 2(3) + 1, which means we set n = 3. When we square it, 72 = 49. The proof is correct because 49 is odd.
3
Which algebraic expression depicts an odd number?
Geometric Proof - Examples included
Geometric proof involves the use of shapes, angles and properties of figures to prove a statement. You can't just work with numbers and algebra for this proof. Geometric proof involves logical reason and known theorems to justify results.
Key techniques
You need to understand the following topics in geometry to tackle geometric proof questions:
- Angle rules - This includes the angles in a triangle, angles on a straight line and opposite angles.
- Congruent triangles - Prove two triangles are identical using SSS, SAS, ASA, AAS and RHS rules.
- Circle theorems - The key properties of circles, including angles in a semicircle and opposite angles in a cyclic quadrilateral.
Example 1: Proof with angles
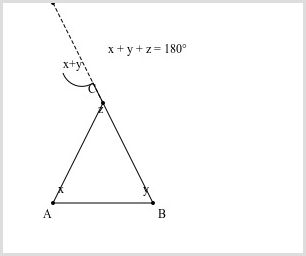
Prove the sum of the angles in a triangle is always 180 degrees.
- Draw a triangle ABC and extend one side.
- Label the three angles inside the triangle x, y and z.
- You should see that x and y are adjacent to an exterior angle. This means: x + y + z = 180 degrees.
- This logic applies to all triangles, which means the sum of the angles in a triangle is always 180 degrees.
Example 2: Proof with congruent triangles
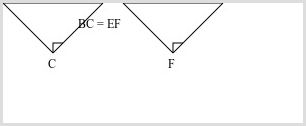
Prove that two right-angled triangles with equal hypotenuses and one matching side are congruent (have the same size and shape).
- Consider two right-angled triangles ABC and DEF. The hypotenuse is AB = DE. The one matching side is BC = EF.
- They share a right angle so we can use the RHS (Right-Angle, Hypotenuse, Side) rule. This confirms the triangles are congruent.
Example 3: Proof with a circle theorem
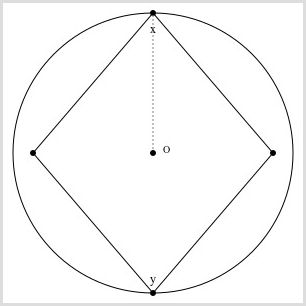
Prove that opposite angles in a cyclic quadrilateral add up to 180 degrees.
- Draw a cyclic quadrilateral (a four-sided shape inside a circle).
- Label the opposite angles as x and y.
- Use the circle theorem: the angle at the centre is twice the angle at the circumference.
- This confirms the rule because x + y = 180 degrees.
4
What is always true about a cyclic quadrilateral?
Common mistakes
1. Assuming a statement is true
People misunderstand what a math proof is. Testing a few examples is not a proof because it does not guarantee a statement will be true in all cases (the exception being proof by exhaustion).
An example claim for you to prove is "The sum of two prime numbers is always even". A student may answer in the following form:
- 3 + 5 = 8 (even)
- 7 + 11 = 18 (even)
This is correct in these exams. However, another example is 2 + 3 = 5, which is odd. This shows the claim is false and underscores the importance of using a proof rather than just testing numbers.
2. Incorrectly express even & odd numbers
You must use the correct algebraic representations to prove number properties. If there are mistakes in your expressions, this will lead to incorrect proofs and lost marks in exams. For example:
- Write an even number as n+2 - You should write 2n, where n is an integer e.g. 2 x 5.
- Write an odd number as n+1 - You should write 2n + 1, which means it will always return a number one greater than an even number e.g. 2 x 23 + 1 = 47.
3. Using factorisation inaccurately
Factorising can prove divisibility statements. It is common for students to apply factors incorrectly. For example, a claim in an exam could be "The sum of two even numbers is always even":
- A mistaken proof would be 2n + 2m = 2n + 2m. This is a correct step but it doesn't show the final proof.
- Using factorisation, the answer is 2n + 2m = 2(n + m).
- This confirms the sum is always a multiple of 2 and an even number because n + m is an integer.
4. Forgetting a conclusion
You need to show your conclusion. Even if your algebra is correct, you risk losing marks with this simple omission.
For example, a student may end the proof with calculations but not state what they prove. You should always summarise the result and link it to the question. An example of the correct approach is below:
"The result can always be written as 2k + 1, where k is an integer. This means the number is always odd."
5
What is the algebraic proof for an odd number?
Why Proof Matters
Mathematical proof is important in higher education, technology and real-world applications. The ability to construct logical arguments and justify conclusions is a valuable skill that extends beyond GCSE Maths. We have covered some of the uses of math proofs below.
1. Proof in advanced mathematics
The importance of proof becomes greater when studying maths at a higher standard, such as A-Level or university. New topics build on algebraic and geometric proof, including proof by induction and formal logic. For example:
- A-level Maths - Proof is used in calculus to derive differentiation formulas.
- University - Proof is used in a mathematics degree to establish theorems in algebra, geometry and number theory.
2. Proof in computer science & cryptography
Encryption methods in computer science and cybersecurity rely on mathematical proof to secure data. Modern techniques like RSA - which is used for online security - wouldn't be possible. For example:
- Cryptography - Online banking security depends on the proof that certain mathematical functions are difficult to reverse.
- Algorithms - Computers use proof-based logic to check that programs work correctly.
3. Proof in science & engineering
Physics, engineering and architecture rely on mathematical proof and the ability to logically justify a result. This proof-based reasoning is used by scientists to verify equations. Engineers rely on mathematical models to design safe structures:
- Physics - The laws of motion are proven using mathematical models.
- Engineering - Proof is used in design calculations to ensure bridges, skyscrapers and other buildings are structurally sound.
Practice questions
We have listed a few GCSE-style questions to test your understanding of mathematical proof. Try these challenges and check the explanations to see if you were correct. It's a good idea to go further than this sample of exam questions and tackle proof worksheets.
Question 1 - Algebraic proof
Use algebra to prove that the sum of two consecutive odd numbers is always a multiple of 4.
Advice to find the answer:
- Represent the first odd number as 2n + 1.
- Represent the next consecutive odd number as 2n + 3.
- Add them together and simplify: (2n + 1) + (2n + 3) = 2n + 1 + 2n + 3 = 4n + 4
- Factorise your final answer to show that it is a multiple of 4: 4n + 4 = 4(n + 1)
Answer - The sum of both odd numbers is 4n + 4. Factorising gives 4(n + 1), which is a multiple of 4. This means the sum of two consecutive odd numbers is always a multiple of 4.
Question 2 - Geometric proof
Prove the sum of the exterior angles of a polygon will always be 360 degrees.
Advice to find the answer:
- An exterior angle is created by extending a side of the polygon.
- What happens when you walk around a polygon and turn at each exterior angle?
- Can you prove that the total turn always brings you back to your starting point?
Answer - When you extend each side of a polygon and measure the exterior angles, these angles represent the total turning you do when moving around the polygon. A complete turn is 360 degrees. This means the sum of the exterior angles of a polygon is always 360 degrees.
Question 3 - Contradiction proof
Prove there is no largest prime number.
Advice to find the answer:
- Argue the opposite and assume there is a largest prime number. Call this number P.
- Multiply all known prime numbers together and add 1.
- Is the new number divisible by any primes? What contradiction does this lead to?
Answer - Multiply all known primes and add 1. This new number can be divided by any known prime, which contradicts the assumption that P is the largest prime. There is no largest prime number.
6
What is a key step in algebraic proof?
Final thoughts - Proof Maths revision
Mathematical proof helps to build logical reasoning. It is required for higher education in maths and more generally in real-world applications, including computing and engineering.
This guide has explored the different types of proof and typical questions in GCSE Maths. We have gone through algebraic and geometric proof step-by-step, including examples to cement understanding. Common mistakes and pitfalls have been explored and we have discussed the importance of proof in higher education and across different industries.
If you struggled to understand some aspects of the article, it may help to have a refresher on algebra with this article by ThirdSpaceLearning and geometry by BBC Bitesize. If you want to test your understanding, ExamPaperPractice has past papers on math proof.
If you need extra support learning math form, TeachTutti has qualified GCSE Maths tutors. Every tutor is DBS checked and you can learn in-person or online to boost your GCSE revision and your confidence.
This post was updated on 23 Feb, 2025.

