Iteration means to carry out a process in mathematics repeatedly. When you can't solve an equation using normal algebra, you repeat a formula to get closer to the answer. Essentially, it's a process of continually guessing, checking and refining your answer.
This article will explain what the term iteration means and how it works using examples and exam questions that you may come across. Visuals and quiz questions are included to improve your understanding. It is aimed at Maths GCSE across all major exam boards, including AQA and Edexcel. If you need help revising this topic, TeachTutti has verified GCSE Maths tutors who can support you with in-person or online tuition.
What is the Iteration topic?
Iteration means repeating a process. A number is used in a formula, and this mathematical pattern is repeated or iterated until the value starts to settle down. Essentially, it's a case of tweaking the solution until the value is correct.
Why do we use Iteration?
Some equations are overly difficult or even impossible to solve using standard algebra. This is when we turn to iteration, by approaching the solution in a progressive, step-by-step manner.
An example of iteration begins with a starting value of x1 = 2 and the formula x(n+1) = x(n) + 2
We start by putting 2 into this formula. The number that is returned is the next number we place in the formula. We continue this process until we get a better approximation of the answer we need:
- x1 = 2
- x2 = 2 + 2 = 4
- x3 = 4 + 2 = 6
- x4 = 6 + 2 = 8
This pattern continues. We can see the value keeps increasing by 2 each time. The formula given above doesn't lead to a fixed solution. Instead, it shows how iteration can create a simple pattern. In more complex cases, iteration helps values gradually settle on a number, giving a useful approximation.
The Iteration formula
Let's say we're given the following equation: x2- 3x + 2 = 0.
We'd normally solve it using the quadratic formula or by factorising. We can try a different approach if this can't be done easily: rearranging the equation using iteration:
- Start with the formula x2 - 3x + 2 = 0
- Rearrange this to make x the subject. For example: Rearrange it to make x the subject. One possible rearrangement is x = square root (3x - 2)
- We now have the following formula that we can use for iteration: x(n + 1) = square root (3x(n) - 2)
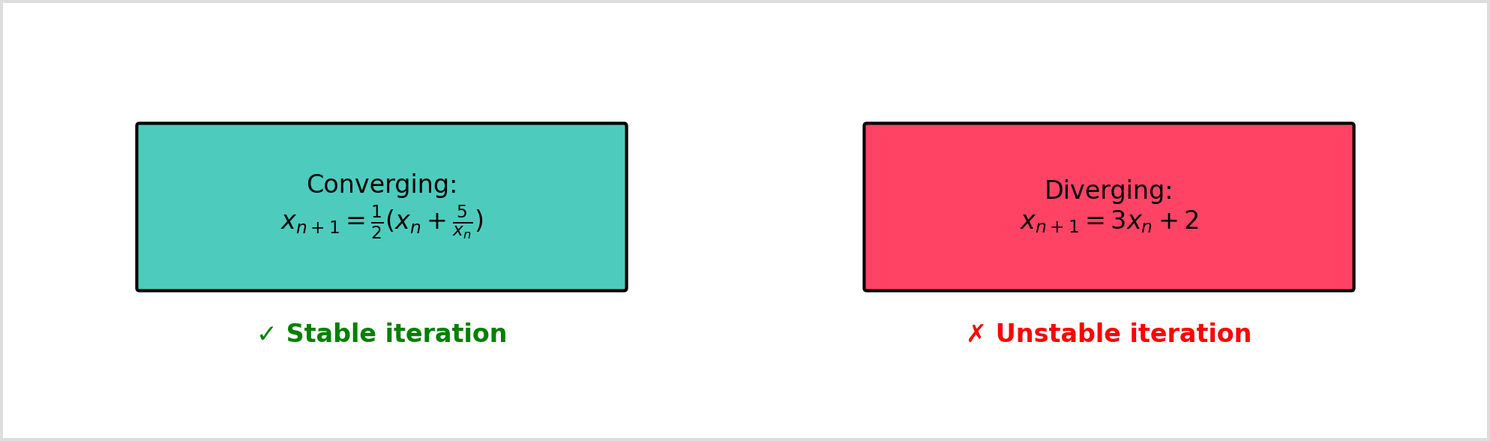
Remember that iteration should mean the numbers converge towards a fixed point. It won't always work after you've rearranged the equations. Sometimes, a formula will cause the numbers to spiral out of control.
If the numbers jump all over the place or continue to endlessly expand, this means the iteration is diverging. Normally, you will be given the formula in your exam questions, so this won't be an issue. However, it's important to bear in mind that iteration can fail, which is known as divergence.
Solved examples
We have gone through an example step-by-step below to improve your understanding of the process called iteration.
We will use the following formula: xn + 1 = 1 / 2(xn + 5 / xn)
We have a starting value of x1 = 2, and we need to find x2, x3 and x4. The answers need to be to 4 decimal places.
This formula is one of the oldest examples of iteration. It helps us to approximate the square root of 5.
- Start with your initial value - x1 = 2
- Put the number into the formula - x2 = 1 / 2 (2 + 5 / 2) = 1 / 2 (2+2.5) = 1 / 2 (4.5) = 2.25
- Keep going through the iterations - x3 = 1 / 2 (2.25 + 52.25) = 1 / 2 (2.25 + 2.2222) = 1 / 2 (4.4722) = 2.2361. x4 = 1 / 2(2.2361 + 52.2361) = 1 / 2 (2.2361 + 2.2360) = 1 / 2 (4.4721) = 2.2361
- Look for convergence - the values are starting to repeat. This means the iteration is working. We are closing in on the square root of 5, which is approximately 2.2361.
| xn | Value of xn | Formula substitution |
| 1 | 2.0000 | 1 / 2(2 + 5 / 2) = 2.2500 |
| 2 | 2.2500 | 1 / 2(2.25 + 5 / 2.25) = 2.2361 |
| 3 | 2.2361 | 1 / 2 (2.2361 + 5 / 2.2361) = 2.2361 |
| 4 | 2.2361 | 1 / 2 (2.2361 + 5 / 2.2361) = 2.2361 |
Graphical illustration of Iteration
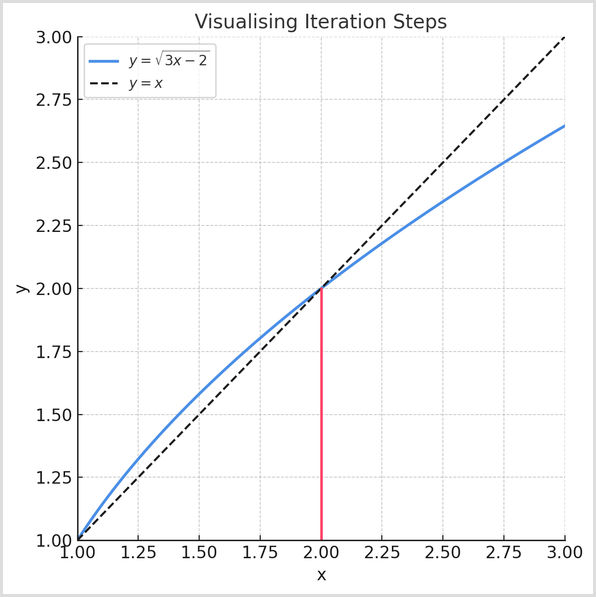
You can visualise the process of iteration in a graph, which can help you to learn this topic. For example, let's say we have the following formula: x(n+1) = square root (3x(n) - 2)
We can plot the two functions and turn them into a graph:
- The iteration formula is y = square root (3x - 2)
- The line we will use to bounce values back and forth is y = x. Wherever a function crosses this line is where x = f(x). This means we have found a solution - a fixed point where the value stops changing.
Visualising steps in Iteration
You can see iteration by moving between the curve and the line. It will create a staircase or spiral, depending on the formula you use:
- Start on the x-axis with your initial value.
- Go vertically up to the curve, which represents the formula.
- Go horizontally across to the dotted line (y = x).
- Repeat this action by going up to the curve and across to the line.
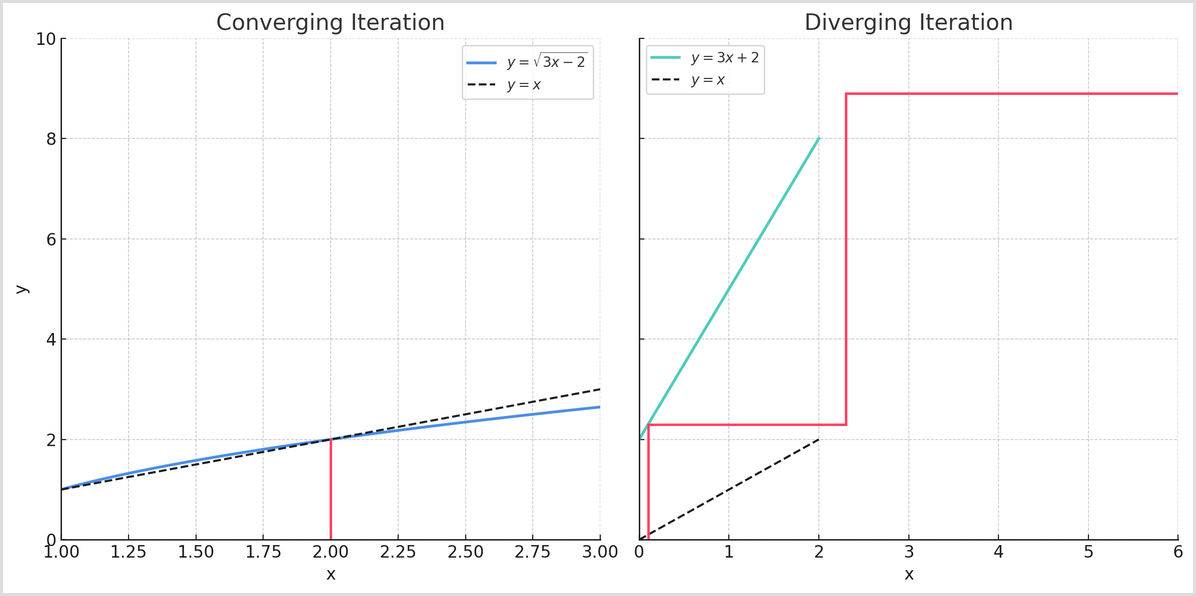
Converging vs diverging
The iteration is converging when the steps get smaller and spiral in. This means you are closing in on a solution. If the steps spiral out or bounce away, this means it is diverging, and iteration won't help you to solve the equation.
You don't have to draw these graphs in the exam. However, they are a useful as a guide to why iteration works with some formulas, while creating divergence with other formulas.
Why Iterative methods can fail
Iteration relies on the values approaching a fixed point over repetitions. This is not guaranteed and only happens under certain conditions. If these conditions aren't met, the values produced will grow increasingly inaccurate. This behaviour is called divergence.
Divergence happens when the values created by the iteration formula move away from a solution. The reasons for this include:
- The starting value is too far from the fixed point.
- The arrangement of the formula doesn't promote convergence.
- The gradient/rate of change in the function is too steep near the fixed point.
A divergent sequence could oscillate back and forth without settling. It may change size indefinitely, growing larger or smaller. Divergence may also initially seem to settle down before moving away again.
It's a good idea to test a few values when using an iterative method. Observe the pattern and don't assume it will naturally converge. The process is workings is the values appear to settle towards a number. If the values increase rapidly, repeat erratically or move from a target value, the iteration is diverging.
You will normally be given an iteration formula that converges. However, understanding divergence is important when interpreting graphs and spotting incorrect results during your workings.
Quiz questions
Theory questions
1
Why is the iteration formula used to solve equations?
2
What starting value is likely to cause divergence?
3
Why could convergence fail with the iteration formula xn + 1 = 3xn + 2 fail to converge?
Visual questions
4
Which graph shows iteration convergence on a solution?
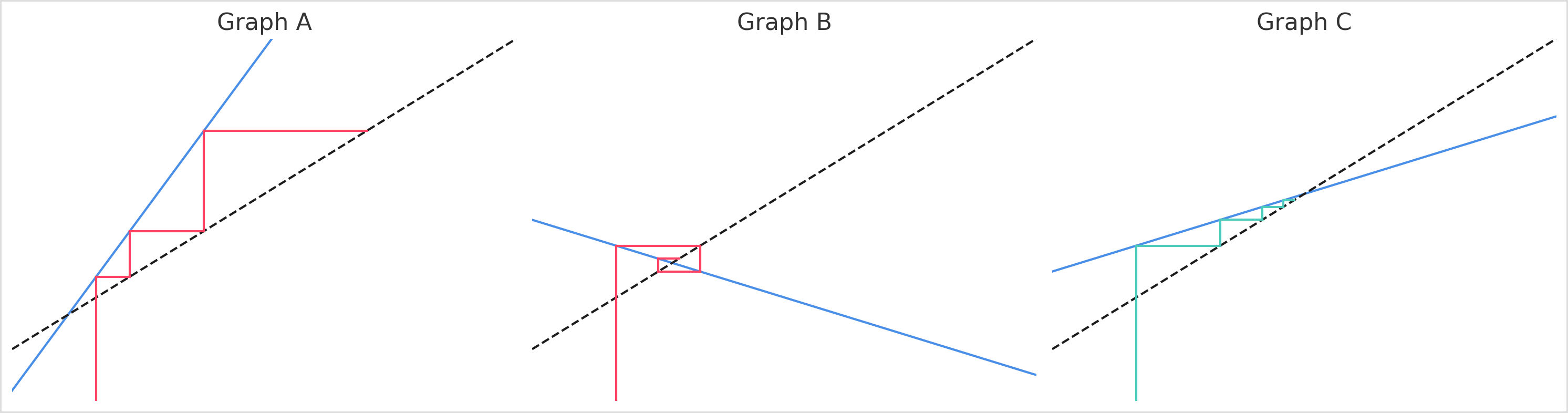
5
Which table follows the formula xn + 1 = 1 / 2(xn + 5 / xn)?

6
Which graph shows a suitable fixed point for iteration?
Exam questions - GCSE Maths
Iteration is assessed as part of the Algebra topic within GCSE Maths. Questions will often apply an iteration formula. You will be asked to interpret results and show a solution lies between two values.
The typical question format in your exams will fall into one of the following categories:
- Find the solution to a certain number of decimal places using a given formula.
- Use substitution and sign change to show that a root lies between two values.
- Explain why the result is a solution or why an equation has no solution within a certain range.
Exam guide and common mistakes
You will be awarded marks for the following in your workings and final answer:
- Correctly using the iteration formula. This includes substitution.
- Consistent rounding, normally to 3 decimal places.
- Showing your workings clearly. This is especially important when you are calculating if the value satisfies the given equation.
- A displayed final answer. Units are shown if relevant (e.g. grams or metres).
The following are common mistakes to watch out for, which will lead to deducted marks:
- Rounding too early in the workings. This can result in incorrect answers.
- Copying the formula incorrectly or substituting the wrong value.
- When it is a root question, always check that the final satisfies the original equation.
Worked exam questions
In both of the example questions below, you are expected to calculate step-by-step and show the results to 3 decimal places. The final answer should normally be presented in a table or list.
Exam questions - 1
The iteration formula is: x(n + 1) = (1/2) (x(n) + 10 / x(n))
Use this formula and start with an initial value of x(1) = 3.
Calculate the next three values of x: x(2), x(3), and x(4). The answer must be to 3 decimal places.
Exam question - 2
Use following the iteration formula to find x2, x3 and x4, where x1 = 3:
xn+1 = 1 / 2(xn + 10 / xn)
The answer must be to 3 decimal places.
Conclusion - Iteration revision
Iteration is a method for finding approximate solutions to equations that can't be solved by algebra. You begin with a starting value and run the formula repeatedly until the values converge on a solution. We have explored how to rearrange equations to create an iterative formula, how to interpret graphical patterns of convergence/divergence and when the process is stable as opposed to when it diverges.
Iteration is often assessed both numerically and graphically in GCSE exams. To improve your understanding, we recommend practising with worked examples and exam-style questions. MathGenies has iteration worksheets. You may also want to read up on algebraic manipulation by Brilliant to support your understanding of this topic.
If you need further support, TeachTutti has DBS-checked GCSE Maths tutors who can help with iteration and other key topics. Every tutor is DBS checked. You can learn in person or online, and they will tailor lessons to your needs, such as preparing revision notes.
This post was updated on 09 Jul, 2025.

