The Highest Common Factor (HCF) and Lowest Common Multiple (LCM) simplify fractions and help to solve equations. They are often used to solve problems involving ratios, schedules and proportions, such as calculating when two recurring events will coincide.
This article is designed to support students with their GCSE Maths revision. It is suitable for all major exam boards, including OCR, Edexcel and AQA. LCM and HCF examples are included and quiz questions are provided to test your knowledge. If you need more support, TeachTutti has experienced GCSE Maths tutors who can help you learn this topic.
Highest Common Factor (HCF)
A factor is a number that divides evenly into another number e.g. the factors of 12 are 1, 2, 3, 4, 6 and 12. The number of factors increases as the number increases in value. For example, the factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
The Highest Common Factor (HCF) is the biggest factor shared between two or more numbers. For instance, let's say the two numbers are 6 and 12. The factors of 12 are 1, 2, 3, 4, 6 and 12. The factors of 18 are 1, 2, 3, 4, 6, 9 and 18. The highest shared factor is 6. Therefore, the HCF of 12 and 18 is 6.
Find the HCF
- List the factors - Find all the numbers that divide into the given number. The numbers must be whole integers. For example, the factors of 8 are 1, 2, 4 and 8, while the factors of 12 are 1, 2, 3, 4, 6 and 12.
- Find the common factors - Find the numbers that are in both lists e.g. the shared factors of 8 and 12 are 1, 2 and 4.
- Identify the largest common factor - The HCF is the biggest common factor e.g. the HCF of 8 and 12 is 4.
Using prime factors
It takes time to list the factors for large numbers. A better approach in this situation is prime factorisation:
- Find the prime factors for each number. For example, the prime factors of 12 are 22 x 3. The prime factors of 18 are 2 x 32.
- Find the common prime factors. In this example, the prime factors are 2 and 3.
- Multiply the common factors to find the HCF: 2 x 3 = 6.
1
What is the highest common factor of 24 and 36?
Lowest Common Multiple (LCM)
A multiple is the result when multiplying a number by an integer e.g. the multiples of 4 begin with 4, 8, 12 and 16.
The Lowest Common Multiple (LCM) is the smallest multiple of two or more numbers. Let's say we need to find the LCM of 10 and 15. The lowest multiples of 10 are 10, 20, 30, 40, 50 and 60. The lowest multiples of 15 are 15, 30, 45, 60, 75 and 90. The common multiples they share are 30 and 60. The smallest will be the LCM, which is 30.
Find the LCM
- List the multiples - Find the first few multiples for each number. For example, the first multiples of 3 are 3, 6, 9, 12, 15, 18, 21 and 24. The first multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56.
- Find the common multiples - Both numbers share the common multiple 21.
- Choose the smallest common multiple - The LCM for 3 and 7 is 21.
Using prime factors
As we mentioned above, prime factorisation is a quicker method when you are using large numbers. It makes sure that no common factors are counted multiple times by mistake:
- Find the prime factors for each number. For instance, the prime factors for 4 are 22 and the prime factors for 6 are 2 x 3.
- Include all the prime factors and use the highest power of each factor (22 x 3 = 12).
- Multiply these factors together. In our example, the LCM of 4 and 6 is 12.
2
What is the lowest common multiple of 8 and 12?
Venn diagrams
Venn diagrams are a visual way to find the HCF and LCM. The diagram shows the prime factors in overlapping circles so that you can easily see the shared and unique factors. A simple example below shows a comparison of fish and whales. The circles show their unique qualities and the overlapping section shows that both swim, live in water and have fins.
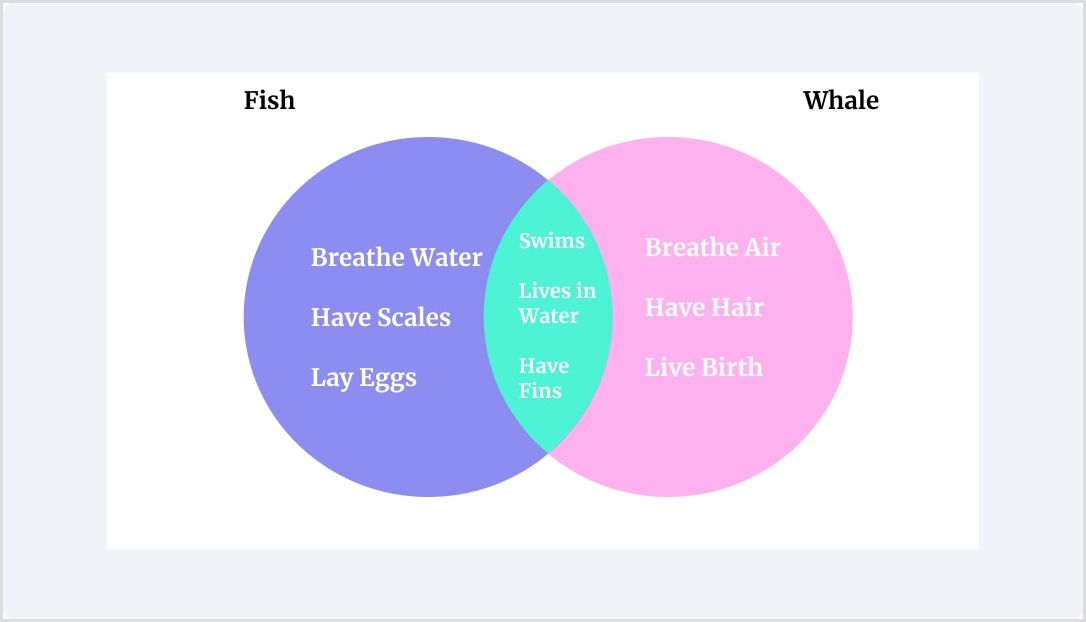
How to Use Venn Diagrams:
- Prime Factorisation - Start by breaking each number into prime factors. For example, the prime factors for 24 are 23 × 3, while the prime factors for 36 are 22 × 32.
- Populate the Venn Diagram - Put the common factors in the overlapping region and the unique factors in the area of each circle that doesn't overlap.
- Calculate the HCF and LCM - The HCF is the product of the factors in the overlapping region of the circles. For example, the overlapping region contains 22 x 3 = 12, so the HCF is 12. The LCM is the product of all factors. In this example, multiply 23 x 32 (from 36) and 2 (from 24). This means the LCM is 72.
You can practice creating Venn Diagrams using the online tool Meta-Chart.
3
Use a Venn diagram to find the HCF and LCM of 18 and 24.
Applications of Highest Common Factor and Lowest Common Multiple
HCF and LCM play an important role in real-life situations, including industries like finance and science. They are commonly used in ratios, proportions and shared events.
Applications of HCF:
- Simplify fractions - HCF reduces a fraction to its simplest form. It divided the numerator and denominator by their HCF. For example, you can simplify 18/24 by dividing both by their HCF of 6. This simplifies the fraction to 3/4.
- Divide resources - HCF finds the largest equal-sized portions or groups. For example, let's say we have 18 apples and 24 oranges. We want to divide them into identical baskets with no leftovers. The HCF of 6 tells us the number of items per basket.
Applications of LCM:
- Scheduling and timetables - We can find coinciding events with the LCM. For example, a bus runs every 18 minutes and a train runs every 24 minutes. The LCM of 18 and 24 tells us when the bus and train arrive at the station together (72 minutes).
- Repeating patterns - LCM finds how frequently repeating cycles align. For instance, two lights will flash together every 12 seconds (the LCM) when one light flashes every 4 seconds and the other flashes every 6 seconds.
4
There are two bells. One bell rings every 12 seconds and the other rings every 18 seconds. How long will it take for them to ring together?
Common mistakes with HCF and LCM
It is easy to make errors when using the highest common factor and lowest common multiple, particularly under exam pressure. We have detailed the common mistakes to watch out for:
- Confuse factors with multiples - Students often confuse factors (numbers that divide into another number) with multiples (numbers created by multiplying another number). Always remember that factors are smaller than or equal to the number, while multiples are equal or greater.
- Missing factors or multiples - A common mistake is forgetting to list all the factors and multiples. Double-check your lists and use prime factorisation when the number is large.
- Overlooking prime factorisation - Ensure that you fully break down each number into its prime factors. Use a factor tree to ensure all prime factors are included (ThirdSpaceLearning has a guide to factor trees).
- Confusing HCF and LCM - Students will sometimes solve the HCF when LCM is needed and vice versa. Check the question carefully: HCF focuses on common factors, while LCM uses common multiples.
- Multiplying incorrectly - Make sure you avoid errors multiplying prime factors for HCR and LCM. Do calculations step-by-step and use a calculation if permitted.
- Skipping Venn diagrams - Venn diagrams are a big help with larger numbers. It takes more time, but it is a useful visual aid that helps you avoid missed factors or duplicates.
Final thoughts
Getting the hang of the Highest Common Factor and the Lowest Common Multiple is an important part of GCSE Maths. They simplify mathematical problems and have real-world uses, such as organising schedules or dividing resources.
As ever, regular practice is the best way to learn this topic. Don't neglect Venn diagrams, which can be a real visual benefit. To test yourself, MathsGenie has HCF and LCM past exam questions.
If you need support getting the hang of HCF and LCM, TeachTutti has DBS-checked and qualified GCSE Maths tutors. You can learn online or in-person with our tutors and they can tailor lessons to address your specific revision goals.

